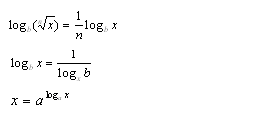Logaritm – definiție

log_b(x) – logaritm în baza b al unui număr real pozitiv x reprezintă puterea la care trebuie ridicată baza b pentru a obţine numărul x.

Condiţiile de existenţă ale logaritmului

• x şi b numere reale pozitive;
• b nenul (b>0);
• b≠1.

Logaritmul zecimal – definiție

Dacă  baza  b=10, atunci avem :

log₁₀(1)=0, deoarece 10⁰=1 => log₁₀(10⁰)=0;

log₁₀(10)=1, deoarece 10=10¹=> log₁₀(10¹)=1;

log₁₀(100)=2, deoarece 100=10² => log₁₀(10²)=2;

log₁₀(1000)=3, deoarece 1000=10³; log₁₀(10³)=3;

Logaritmul în baza 10 se mai numeşte şi logaritm zecimal – log₁₀(x).

Logaritmul natural – definiție

Dacă  baza b=e, unde e=2,7182811828 () atunci avem :

loge(1)=0; deoarece e⁰=1 => loge(e⁰)=0

loge(e)=1; deoarece e=e¹ => loge(e¹)=1

Logaritmul în baza e se mai numeşte şi logaritm natural.

Logaritmul natural se notează cu ln(x).

Graficul functiei logaritm

Proprietatile logaritmilor

log_b(x) = 0, pentru x = 1 – logaritmul are valoarea 0 pentru x = 1 (logaritm din 1 este 0);

log_b(x) > 0, pentru x > 1 – logaritmul are valori pozitive pentru valori ale lui x mai mari decât 1;

log_b(x)< 0, pentru 0 < x < 1 – logaritmul  are valori negative pentru valori ale lui x cuprinse în intervalul (0,1);

log_b(xy) = log_bx + log_by

log_b(x/y) = log_bx – log_by

log_b(xⁿ)=n log_bx

Transformarile logaritmilor

TRANSFORMAREA LOGARITMULUI NATURAL ÎN LOGARITM ZECIMAL

log₁₀(x)=(1/ln10)ln(x)=0,434294ln(x)

TRANSFORMAREA LOGARITMULUI ZECIMAL ÎN LOGARITM NATURAL

ln(x)=(1/loge)log₁₀(x)=2,302585log₁₀(x)

ŢINEŢI MINTE !

– log_b1 – logaritmul în bază b din 1 este egal cu  0 deoarece orice număr ridicat la puterea 0 este egal cu 1;

– log_b0 – logaritmul în bază b din 0 este  – ∞, dacă b>1;

– log_b0 – logaritmul în bază b din 0 este  ∞, dacă b<1;

Un caz  special de logaritm este logaritmul natural.